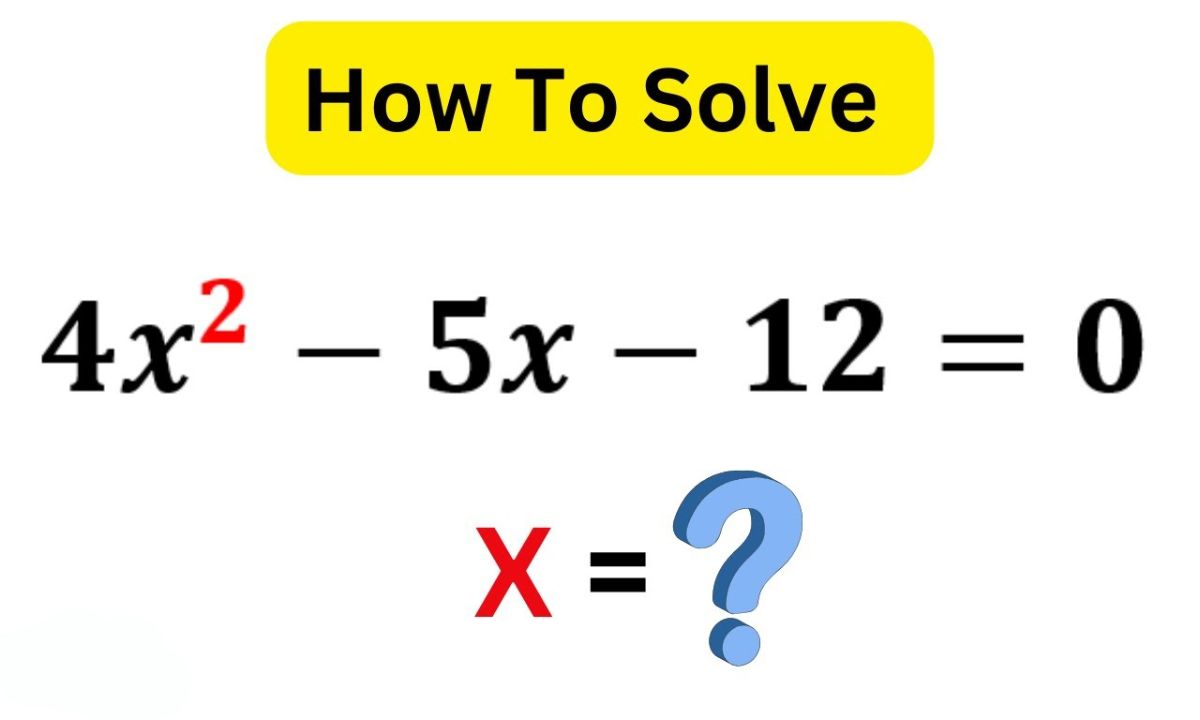Know About Quadratic Equation: 4x ^ 2 – 5x – 12=0

Quadratic equations are fundamental in algebra. They appear in various fields of study. Understanding them is crucial for students and professionals alike. 

The equation 4x^2 – 5x – 12 = 0 is a classic example of a quadratic equation. It serves as an excellent model to explore the properties and solutions of quadratic equations.

Know what are quadratic equations?

Quadratic equations are polynomial equations of the second degree. They involve variables raised to the power of two. The standard form of a quadratic equation is ax^2 + bx + c = 0. In this form, ‘a’, ‘b’, and ‘c’ are constants, and ‘x’ is the variable. The term ‘a’ must not be zero, as this would make the equation linear.

Quadratic equations have numerous real-world applications. They are used in physics to describe motion. In economics, they model supply and demand. Architects use them to design arches and bridges. Even in everyday life, quadratic equations appear in surprising places.

The graph of a quadratic equation is called a parabola. It forms a U-shaped curve. The curve can open upward or downward, depending on the sign of ‘a’. Understanding the shape of this curve is crucial for solving many problems.

Quadratic equations can have zero, one, or two real solutions. These solutions are also called roots. The number of solutions depends on the equation’s discriminant. We’ll explore this concept later in our discussion.

Characteristics of the 4x^2 – 5x – 12 = 0 quadratic equation

Let’s examine our specific equation: 4x^2 – 5x – 12 = 0. This equation has several notable characteristics:

• The coefficient of x^2 is 4, which is positive. This means the parabola opens upward.
• The linear term -5x has a negative coefficient.
• The constant term is -12.
• This equation is in standard form (ax^2 + bx + c = 0).

Comparing our equation to the standard form:

• a = 4
• b = -5
• c = -12

These values are important for solving the equation. They determine the shape of the parabola and the nature of the solutions.

The equation 4x^2 – 5x – 12 = 0 is not a perfect square trinomial. This means we can’t solve it by simply factoring out a common term. We’ll need to use more advanced methods to find its solutions.

Methods to solve quadratic equation: 4x^2 – 5x – 12 = 0

There are several methods to solve quadratic equations. We’ll focus on two popular methods: factoring and the quadratic formula. Both methods have their strengths and are suitable for different situations.

Read This Blog: Get Complete Overview of 127.0.0.1:62893 and 127.0.0.1:49342 IP address

Factoring method:

Factoring is often the first method taught for solving quadratic equations. It involves rewriting the equation as a product of linear factors. Here’s how we can apply the factoring method to our equation:

1. First, we need to find two numbers that multiply to give 4 * -12 = -48 and add up to -5.
2. These numbers are -8 and 3.
3. We can rewrite the middle term using these numbers: 4x^2 – 8x + 3x – 12 = 0
4. Now we can factor by grouping: (4x^2 – 8x) + (3x – 12) = 0
5. Factor out the common terms: 4x(x – 2) + 3(x – 4) = 0
6. Factor out (x – 4): (4x + 3)(x – 4) = 0

Now we can use the zero product property. This property states that if the product of factors is zero, at least one of the factors must be zero. So, we set each factor to zero and solve:

4x + 3 = 0 x = -3/4

x – 4 = 0 x = 4

Therefore, the solutions to our equation are x = -3/4 and x = 4.

Quadratic formula:

The quadratic formula is a powerful tool for solving any quadratic equation. It’s especially useful when factoring is difficult or impossible. The formula is derived from completing the square on the general form of a quadratic equation.

The quadratic formula states that for an equation in the form ax^2 + bx + c = 0, the solutions are given by:

x = [-b ± √(b^2 – 4ac)] / (2a)

Let’s apply this formula to our equation 4x^2 – 5x – 12 = 0:

a = 4 b = -5 c = -12

Plugging these values into the formula:

x = [5 ± √((-5)^2 – 4(4)(-12))] / (2(4)) x = [5 ± √(25 + 192)] / 8 x = [5 ± √217] / 8 x = (5 ± 14.73) / 8

This gives us two solutions: x = (5 + 14.73) / 8 ≈ 2.47 x = (5 – 14.73) / 8 ≈ -1.22

These solutions are approximate due to the square root. The exact solutions are:

x = (5 + √217) / 8 x = (5 – √217) / 8

You might notice that these solutions look different from those we found by factoring. However, they are equivalent. 

The factoring method gave us exact fractions, while the quadratic formula gives us expressions involving square roots.

Frequently Asked Questions

What is the discriminant of a quadratic equation?

The discriminant is b^2 – 4ac. It determines the nature of the roots. A positive discriminant indicates two real roots, zero means one real root, and negative implies complex roots.

Can all quadratic equations be solved by factoring?

No, not all quadratic equations can be factored easily. Some require the quadratic formula or other methods for solving.

What does the graph of a quadratic equation look like?

The graph of a quadratic equation is a parabola. It’s a U-shaped curve that can open upward or downward depending on the sign of the coefficient ‘a’.

How many solutions can a quadratic equation have?

A quadratic equation can have zero, one, or two real solutions. It always has two complex solutions, which may or may not be real.

What’s the difference between roots and solutions of a quadratic equation?

Roots and solutions are the same thing. They are the x-values that make the equation true when substituted into it.

Conclusion

Quadratic equations are a fundamental concept in algebra. They have wide-ranging applications in various fields. The equation 4x^2 – 5x – 12 = 0 serves as an excellent example to understand the properties and solving methods of quadratic equations.

We explored two main methods for solving this equation: factoring and the quadratic formula. Each method has its advantages. Factoring can provide exact solutions in fraction form. The quadratic formula is more general and can solve any quadratic equation.